sTanisha Pal Singh

6 March 2019

Tanisha Pal Singh

1st block

3rd May 2019

Formula for volume of sphere is 4÷3× pie× r^3, where r is the radius of sphere. So the volume of a hemisphere would be 1÷2 × 4÷3 ×pie× r^3 and if we simplify it, it would become 2÷3× pie× r^3, given that r is radius. I feel that the easiest volume to solve is cylinders, spheres and rectangular prism and the hardest to solve is prisms and pyramids.

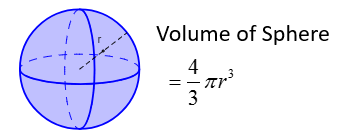
Tanisha Pal Singh

1st block

1st May 2019

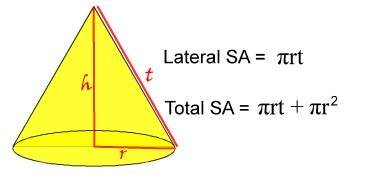
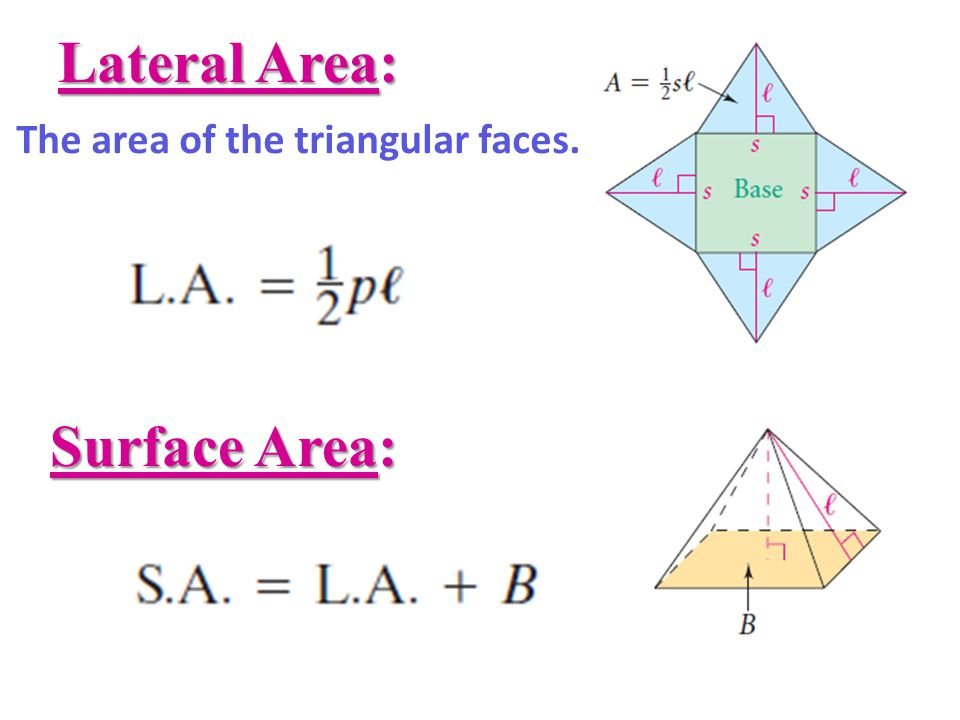
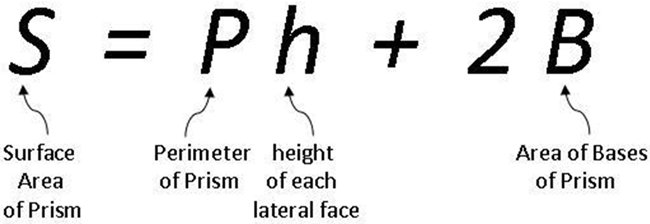
Formula for surface area of Prism is L + 2B, where L is lateral area which we can get by multiplying P and h( perimeter and height) and and B is the area of base. Surface area of cylinder is 2× pie× r× height + 2× pie× r^2, where r is radius and h is height of cylinder. Lateral area of pyramids is 1÷2 × P× l, where L is slant height and P is perimeter. The lateral area of cone is pie× r× l and surface area is pie× r× l+ pie× r^2), where r is radius and l is slant height. I feel the hardest to solve is prisms and easiest is pyramids.

Tanisha Pal Singh

18 April 2019

1) a) NK would be half of 34 as diagonals bisect each other. b) JL would be twice of 11 because of same reason. c) We can find out KL using Pythagorean theorem as KNL forms 90. d) JKM would be 44 as diagonals bisect angles also. e) JML would be 88 as opposite are congruent and JKL formed 88. f) We can find out MLK by subtracting 88 from 180 as consecutive angles are supplementary. g) MNL would be 90 as diagonals in rhombus are perpendicular. h) KJL would be 46 as it is equal to MLJ which is 46.

2) a) All sides are same in square and ZY is equal to WZ which is 24. b) WY is 33.9 we can find out using Pythagorean theorem. c) RX would be half of 33.9 which is 16.95 as diagonals are equal and also bisect. d) WRZ is 90 as ZWR and WZR are 45. e) XYZ is 90 as all angles of square are 90. f) ZWY is 45 as it’s angle was bisected by diagonal.

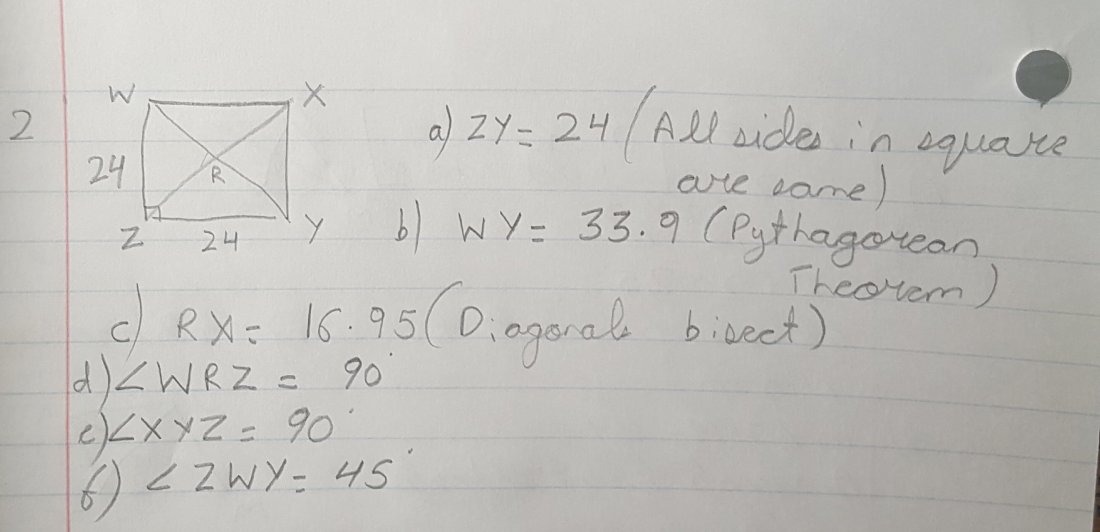
3) Two angles are congruent so we will set them equal. We will find x and plug in the value and then find FCD.

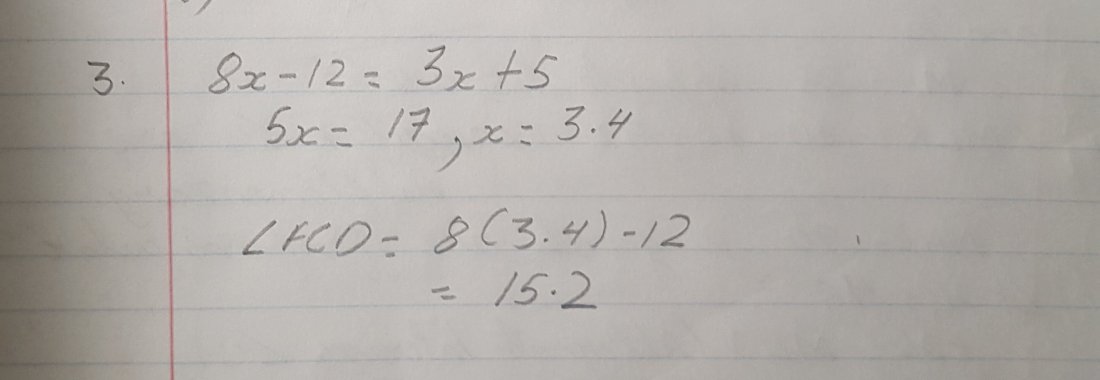
Tanisha Pal Singh

17 April 2019

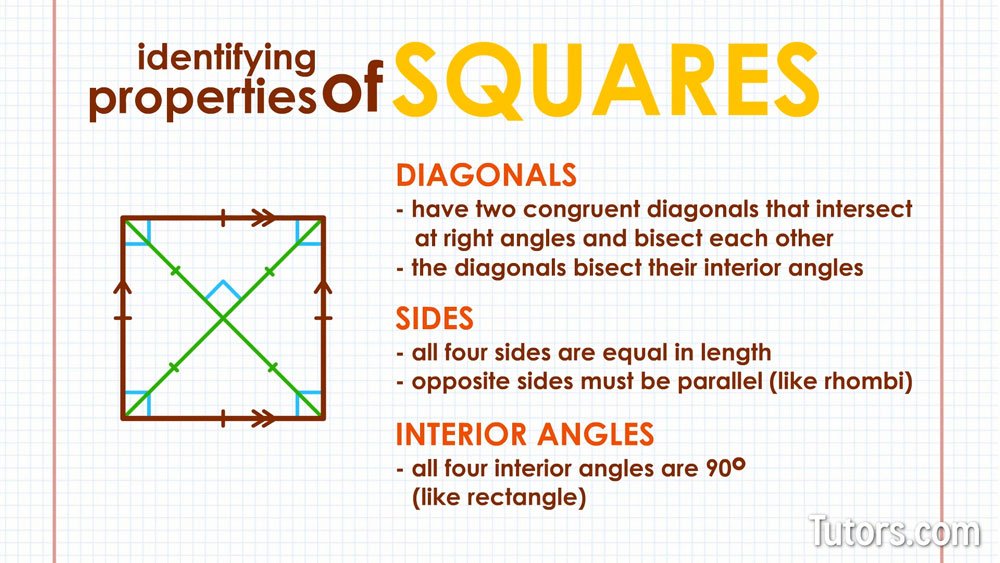
A square is a quadrialteral which has all four sides equal and four right angles. It has diagonals equal and diagonals bisect each other and angles. Consecutive angles are supplementary and opposite angles are equal. Diagonals are perpendicular.

Trapezoid- It is a quadrialteral with one pair of parallel sides. Consecutive angles are supplementary. There is a midpoint which connects the legs. There is another type of trapezoid called isoceles trapezoid in which it’s non parallel sides are congruent. Diagonals, base angles are congruent and oppsite angles are supplementary.

Tanisha Pal Singh

12 April 2019

A rectangle is a type of parallelogram with four right angles. It has opposite sides equal and parallel. The diagonals bisect each other. Opposite angles are equal and consecutive angles are supplementary.

Example 6- We can find out whether it is a rectangle or not using distance formula. We will find the distance between each four line segments and the diagonals. Opposite sides have equal distance and diagonals also have equal distance. Hence it is a rectangle.

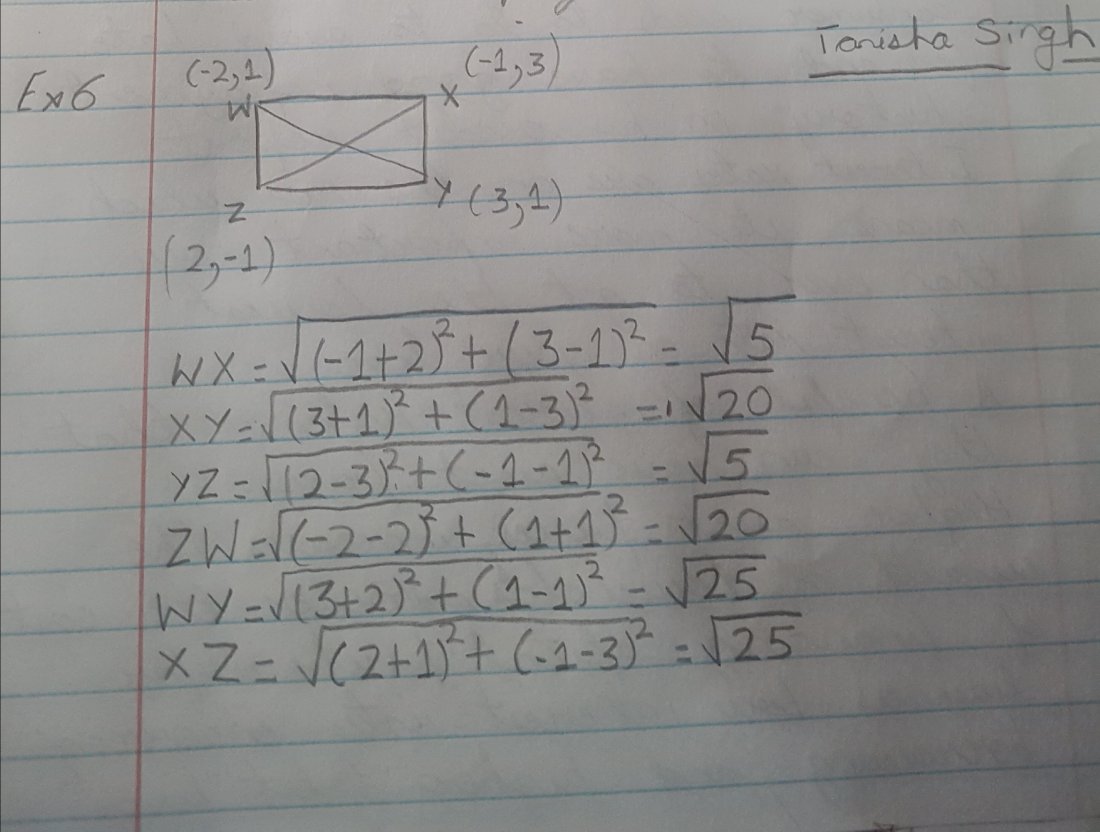
Tanisha Pal Singh

5 April 2019

Angles of a Polygon- The sum of the measures of the interior angles of a polygon with n sides is (n- 2) ×180. The sum of the measures of the exterior angles of a polygon is always 360.

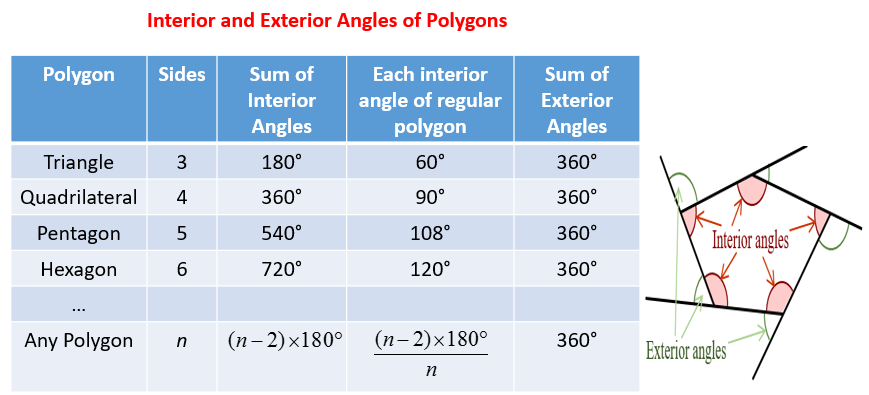
Parallelograms- A parallelogram is a simple quadrialteral with two pairs of parallel sides. The opposite sides are equal in measure and opposite angles are equal in measure and consecutive angles are supplementary.

Tanisha Pal Singh

29 March 2019

In my spring break, I went to Memphis, Nashville, Chattanooga and Helen with my parents. In Memphis, I did a tour of Elvis Presley’s mansion and studio. In Nashville, we stayed for a few hours and visited all the good places and then we went to Chattanooga.

In Chattanooga, I saw a place from where we can see 7 States of U.S.A. including Georgia, Alabama, Tennessee, South Carolina, North Carolina, Kentucky and Virginia. That place was at the top of the mountain so we had to climb. We also did Inclined mountain adventure. Then we went to Helen and we did very much trekking and climbing over there to see three waterfalls.

This is me at the mountain from where we can see seven States

This is me in front of a monument which is located in the outskirts of Memphis.

Tanisha Pal Singh

13 March 2019

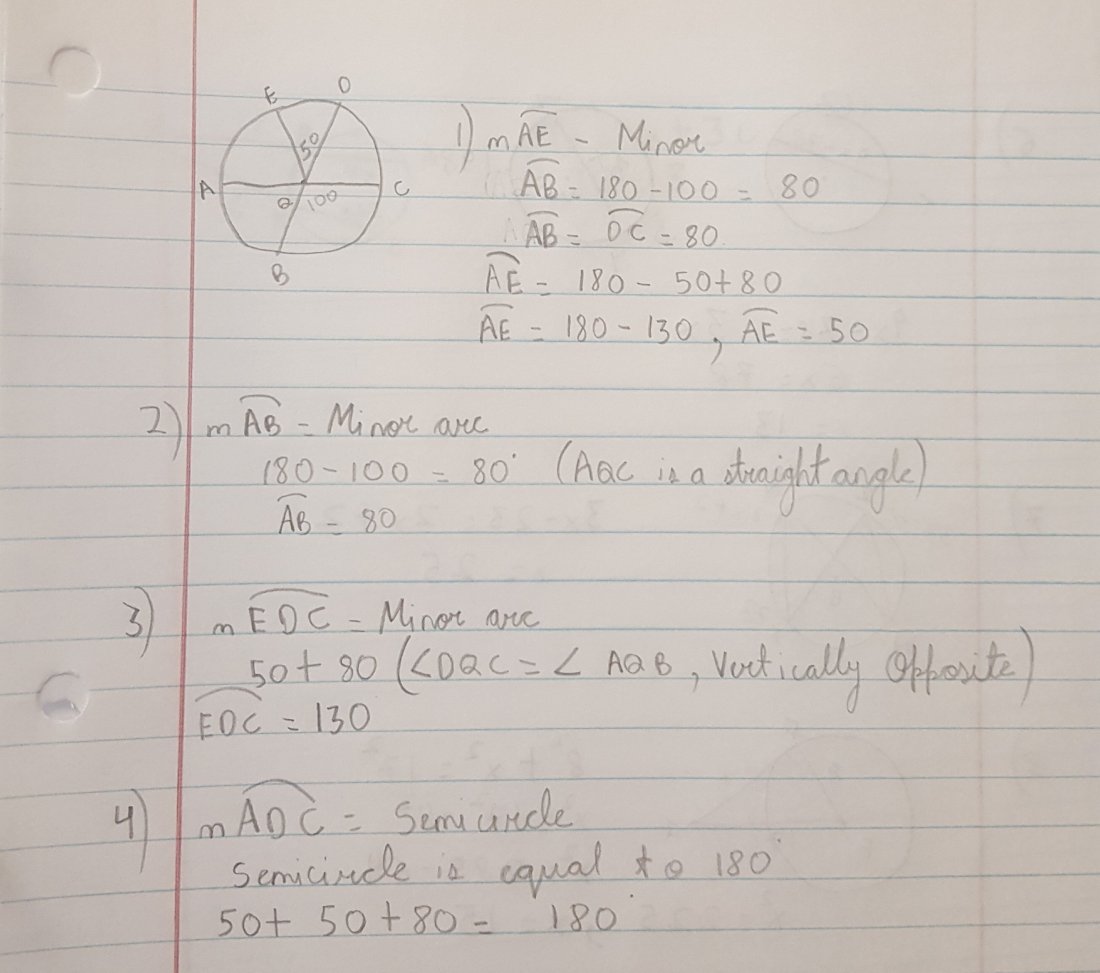
1) Arc AE is a minor arc because it is less than 180. We will find out it’s measure angle AQB by subtracting 100 from 180 as AQC is a linear pair. Angle AQB is 80. AQB and DQC are vertically opposite. So DQC is also 80. Now, we can find out AQE by first adding 50 and 80 which would give us 130 and then we will subtract that from 180. So AQE is 50 and Central angle is equal to its arc. So arc AE is 50.

2) AB is a minor arc because it’s measure is less than 180. We know that AQC is straight angle. So we can subtract 100 from 180 which is 80. AQB is equal to arc AB which is 80.

3) Arc EDC is also a minor arc as it is less than 180. We know DQC and AQB are vertically opposite. So DC is 80 and ED is 50. We will add those which is 130 which is arc EDC.

4) Arc ADC is a semicircle because it’s endpoint are on endpoints of diameter. Semicircle is always equal to 180 but we can find that by adding AQE, EQD and DQC. So 50+50+80 which is 180.

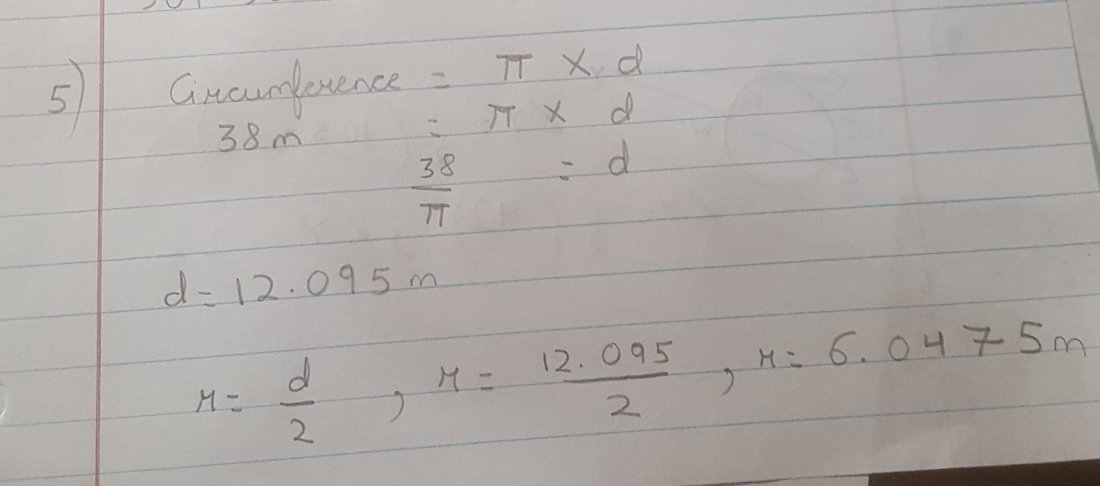
5) We have to find out diameter and radius. We know circu.ference is the product of pie and diameter. We will put the values in equation. So 38 m is equal to pie and diameter. Sister is equal to 38 divided by pie. So diameter would be 12.095 m. We know radius is the half of diameter. So we will divide 2 by 12.095 m which would give us the radius as 6.0475 m.

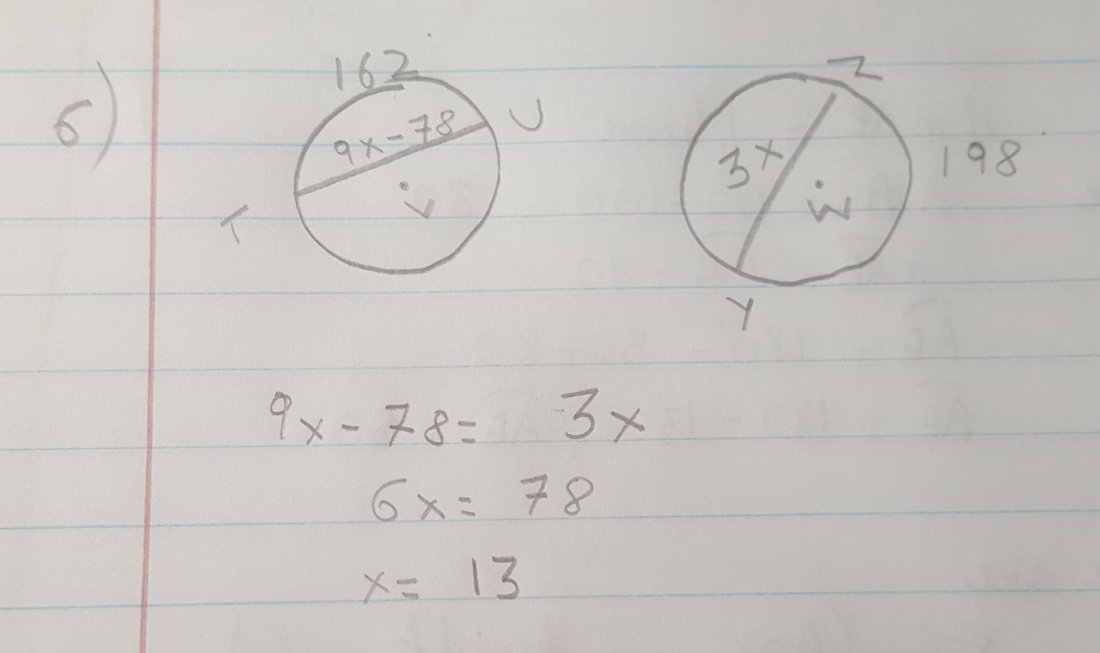
6) The circles are congruent to each other and arc are also congruent because 360- 162 is 198. So the chords are also congruent. We have to solve for x. We will set 9x-78 and 3x equal to each other. We will put variables on one side and numbers on other. So +3 would subtract on going on left side and -78 would become +78. So 6x is equal to 78. x is equal to 13.

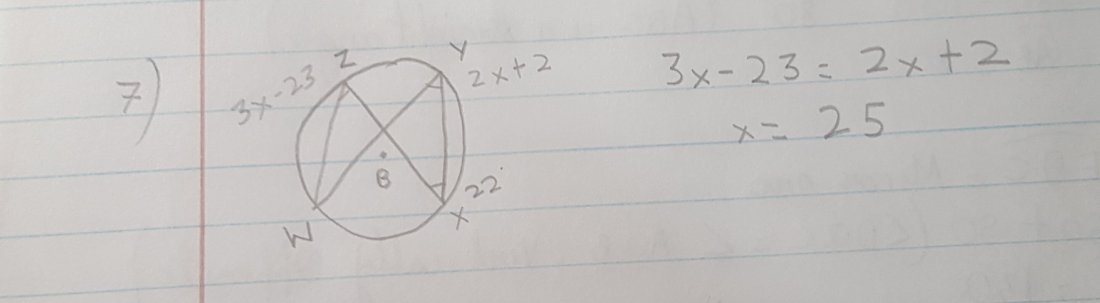
7) We know that if two Inscribed angles of a circle intercept the same arc or congruent arcs, then the angles are congruent. So we will set 3x-23 and 2x+2 equal to each other and solve for x. 2x would subtract on left side and -23 would add on right side. So x is equal to 25.

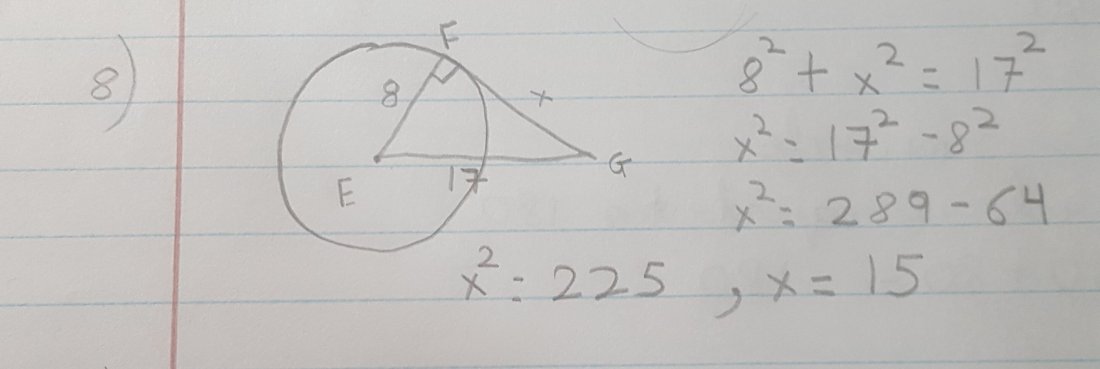
8) We have to solve for x. Where a radius meets a tangent it forms 90 degree. So 17 is hypotenuse. So 8^2 + x^2 = 17^2. So x^2 would be equal to 289- 64 which would be 225. We will do square root of 225 which would give us x as 15.

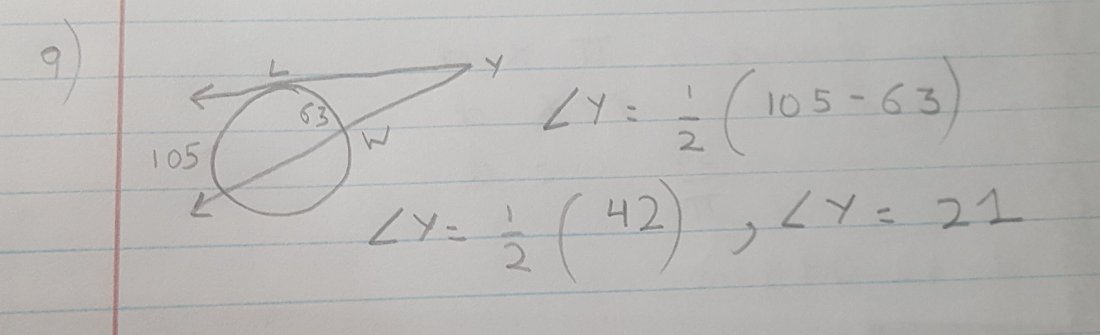
9) If two intersecting secants meet on the exterior of the circle, the angle formed by two secants outside is half the measure of big arc- small arc. So angle Y would be 1÷2 (105- 63), 1÷2 × 42. So angle Y would be 21.

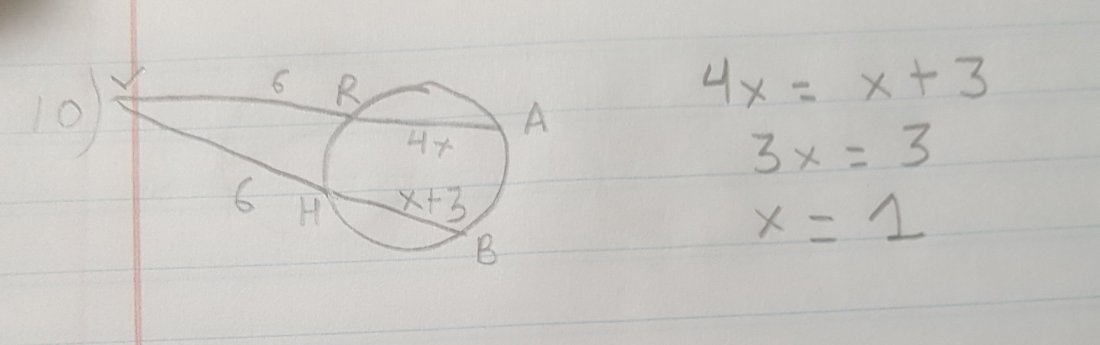
10) The outside of the circle is equal so we can set 4x and x+3 equal to each other. So 4x= x+3

3x= 3. x=1

Tanisha Pal Singh

7 March 2019

A secant is a line that intersects a circle at exactly two points. If two chords intersect a circle, then the products of the lengths of the chord segments are equal. If two secants intersect in the exterior of a circle, then the product of the measures of one secant segment and it’s external secant segment is equal to the product of the measures of the other secant and it’s external secant segment.